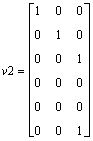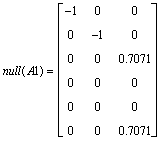Bug in MATLAB?: Increment shortcut in a loop (ex. ++i;)

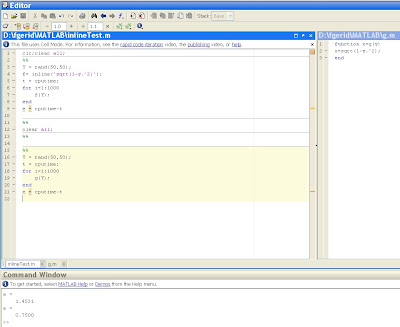
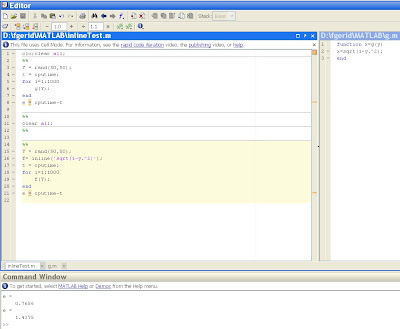
Today, i used an increment shortcut in a  MATLAB simulation loop. Surprisingly i realized that MATLAB accepts the increment shotcut (++variable) without any warning but it does not increase the variable's value in the loop, it remains the same as  the value that was initialized to.
However as an active Octave user in Ubuntu, this usage of the shortcut was just a programming practice for me and it always worked fine. Actually, as far as i understood from the MATLAB Central, these shortcuts are not implemented in MATLAB. But my point is not the absence of implementation, my point is the absence of warning (or error might be in this case) on the usage of the unimplemented increment shortcut.
It can be called as a bug because a permitted shortcut usage does not work properly at least.

Screeshot from Octave:

Screenshot from Matlab:

Inline defined function in OCTAVE works faster! (Was slower in MATLAB)

Previous example in MATLAB was concluded the Inline defined function was working slower than the same function defined in a ".m" file .

But if you try the same example in GNU Octave 3.2.2 you'll surprisingly see that inline defined function in Octave works faster.

On the other hand, it was not the aim of the work but Octave works faster than MATLAB for this case.

Testing "inline" function speed in MATLAB

A function defined as a seperate m-file works faster than inline function of MATLAB.

Eigenvector Calculation with MATLAB vs Mathematica

We have realized that eigenvector calculation for a square matrix whose eigenvalues are all zero must be done by symbolic toolbox in MATLAB. Otherwise MATLAB gives the wrong answer. Or, you can use Mathematica instead. Since Mathematica is able to calculate eigenvectors numerically for this case.

Here is the example:

Consider such a 6x6 square matrix:

In MATLAB, try to calculate eigenvectors numerically:

%% Eigencvector calculation:: Directly numerical

A1=[0 0 0 0 1 0;0 0 1 1 0 -1;0 0 0 0 0 0;0 0 0 0 0 0;0 0 1 0 0 -1;0 0 0 0 0 0];

[v1,l1]=eig(A1)

Matlab gives eigenvectors as:

which is wrong!.

However by symbolic toolbox:

%% Eigencvector calculation: Using symbolic toolbox

A2=sym([0 0 0 0 1 0;0 0 1 1 0 -1;0 0 0 0 0 0;0 0 0 0 0 0;0 0 1 0 0 -1;0 0 0 0 0 0]);

[v2,l2]=eig(A2)

That's now ok!

%% Cross checking with "null space" concept

%Altough we define matrix numerically, null space of A1 however gives numerically true eigenvector familiy:

null(A1)

And finally here is the Mathematica screenshot:

Mathematica calculates successfully: