Eigenvector Calculation with MATLAB vs Mathematica

We have realized that eigenvector calculation for a square matrix whose eigenvalues are all zero must be done by symbolic toolbox in MATLAB. Otherwise MATLAB gives the wrong answer. Or, you can use Mathematica instead. Since Mathematica is able to calculate eigenvectors numerically for this case.

Here is the example:

Consider such a 6x6 square matrix:

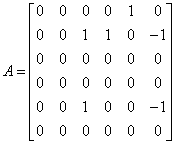
In MATLAB, try to calculate eigenvectors numerically:

%% Eigencvector calculation:: Directly numerical

A1=[0 0 0 0 1 0;0 0 1 1 0 -1;0 0 0 0 0 0;0 0 0 0 0 0;0 0 1 0 0 -1;0 0 0 0 0 0];

[v1,l1]=eig(A1)

Matlab gives eigenvectors as:

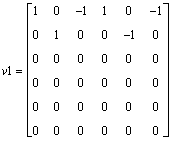
which is wrong!.

However by symbolic toolbox:

%% Eigencvector calculation: Using symbolic toolbox

A2=sym([0 0 0 0 1 0;0 0 1 1 0 -1;0 0 0 0 0 0;0 0 0 0 0 0;0 0 1 0 0 -1;0 0 0 0 0 0]);

[v2,l2]=eig(A2)

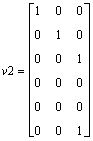
That's now ok!

%% Cross checking with "null space" concept

%Altough we define matrix numerically, null space of A1 however gives numerically true eigenvector familiy:

null(A1)

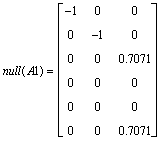
And finally here is the Mathematica screenshot:

Mathematica calculates successfully: